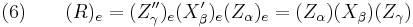Euler angles
The Euler angles are three angles introduced by Leonhard Euler to describe the orientation of a rigid body.[1] To describe such an orientation in 3-dimensional Euclidean space three parameters are required. They can be given in several ways, Euler angles being one of them; see charts on SO(3) for others.
Euler angles also represent three composed rotations that move a reference frame to a given referred frame. This is equivalent to saying that any orientation can be achieved by composing three elemental rotations (rotations around a single axis), and also equivalent to saying that any rotation matrix can be decomposed as a product of three elemental rotation matrices.
Without considering the possibilities of different signs for the angles or moving the reference frame, there are twelve different conventions divided in two groups. One of them is called "proper" Euler angles and the other Tait–Bryan angles. Sometimes "Euler angles" is used for all of them.
Contents |
Definition
Euler angles are a means of representing the spatial orientation of any frame (coordinate system) as a composition of rotations from a frame of reference (coordinate system). In the following, the fixed system is denoted in lower case (x,y,z) and the rotated system is denoted in upper case letters (X,Y,Z).
The definition is Static. Given a reference frame and the one whose orientation we want to describe, first we define the line of nodes (N) as the intersection of the xy and the XY coordinate planes (in other words, line of nodes is the line perpendicular to both z and Z axis). Then we define its Euler angles as:
- α (or
 ) is the angle between the x-axis and the line of nodes.
) is the angle between the x-axis and the line of nodes. - β (or
 ) is the angle between the z-axis and the Z-axis.
) is the angle between the z-axis and the Z-axis. - γ (or
 ) is the angle between the line of nodes and the X-axis.
) is the angle between the line of nodes and the X-axis.
Euler angles between two frames are defined only if both frames have the same handedness. Euler angles are just one of the several ways of specifying the relative orientation of two such coordinate systems. Different authors may use different sets of angles to describe these orientations, or different names for the same angles, leading to different conventions. Therefore any discussion employing Euler angles should always be preceded by their definition.[2]
Unless otherwise stated, this article will use the convention described in the adjacent drawing, usually named Z-X’-Z’’.
Angles signs and ranges
Normally, angles are defined in such a way that they are positive when they rotate counter-clockwise (how they rotate depends on which side of the rotation plane we observe them from. The positive side will be the one of the positive axis of rotation)
About the ranges:
- α and γ range are defined modulo 2π radians. A valid range could be (−π, π].
- β range covers π radians (but can't be said to be modulo π). For example could be [0, π] or [−π/2, π/2].
The angles α, β and γ are uniquely determined except for the singular case that the xy and the XY planes are identical, the z axis and the Z axis having the same or opposite directions. Indeed, if the z-axis and the Z-axis are the same, β = 0 and only (α + γ) is uniquely defined (not the individual values), and, similarly, if the z-axis and the Z-axis are opposite, β = π and only (α − γ) is uniquely defined (not the individual values). These ambiguities are known as gimbal lock in applications.
Conventions
There are two main types of conventions called "proper" Euler angles and Tait–Bryan angles, after Peter Guthrie Tait and George H. Bryan, also known as Nautical or Cardan angles, after Cardan.
Their static difference is the definition for the line of nodes. In the first case two homologous planes (planes overlapping when the angles are zero) are used. In the second one, they are replaced by non-homologous planes (perpendicular when angles are zero).
Nevertheless, it is unusual to use static conventions when speaking about Euler angles. The intrinsic rotations equivalence or the extrinsic rotations equivalence are used instead. According with these equivalences, proper Euler angles are equivalent to three combined rotations repeating exactly one axis. Tait–Bryan angles are equivalent to three composed rotations in different axes.
No information is lost when using the rotation equivalence because the static parameters can be calculated from the name of the convention. For example, given the convention X-Y’-Z’’, the first rotation is perpendicular to "x" and the third one to "Z". Therefore the planes are the yz and the XY, and the line of nodes is the intersection of these two.
Proper Euler angles
There are six possibilities of choosing the proper Euler angles. Using the static definition they correspond to the three possible homogeneous combinations of planes (XY, XZ and YZ) with the two possible options to measure the angles from (given the line of nodes by the XY planes for example, it can be taken X-N or Y-N as first angle). Hence the six possibilities.
There is an intrinsic rotations equivalence which is normally used to name the possible conventions of Euler Angles. If we are told that some angles are given using the convention Z-X’-Z’’, this means that they are equivalent to three concatenated intrinsic rotations around some moving axes Z, X’ and Z’’ in that order. This composition is non-commutative. It has to be applied in such a way that in the beginning one of the intrinsic axis moves together with the line of nodes. The above diagram convention is usually named this way.
Nevertheless, sometimes the extrinsic rotations equivalence could be used. If this is the case, the given angles are backwards, meaning that the first angle is the intrinsic rotation and the last one the precession. The name of the convention would be indistinguishable from the previous one, even if the angles' order is the opposite, being something like z-x-z (here lowercase is used to remark extrinsic composition).
To specify that the given order means intrinsic composition, sometimes a similar notation is used, but stating explicitly which rotation axis are different for each step, as in Z-X’-Z’’. Using this notation, Z-X-Z would mean extrinsic composition.
Tait–Bryan angles
There are also six Tait–Bryan combinations. They come from the two possible non-homogeneous planes that exist when one is given (given XY, there are two non-homogeneous, XZ and YZ). The three possible planes at the reference frame multiplied by the two options for each one yield the six possible conventions.
There are six possible combinations of this kind, and all of them behave in an identical way. Using the intrinsic rotations equivalence, Tait–Bryan angles correspond with the three rotations with a different axis. Z–X–Y for example. There are also six possibilities of this kind. The enclosed image shows the ZXY convention. The other five proper conventions are obtained by selecting different axes of rotation.
These three angles are normally called "Heading, Elevation and Bank", or "Yaw, Pitch and Roll". The second terms have to be used carefully because they are also the names for the three aircraft principal axes.
For Tait–Bryan angles, also intrinsic and extrinsic conventions can be used, giving therefore two meanings for every convention name. For example, X–Y–Z, using intrinsic convention, means that a X-rotation is performed, composing intrinsic rotations Y and Z later, but using extrinsic convention means that after the X rotation, extrinsic rotations Y and Z are performed. The meaning is different in both cases.
Conversion between extrinsic and intrinsic conventions
For either Euler or Tait-Bryan angles, it is very simple to convert from an intrinsic (rotating axes) to an extrinsic (static axes) convention, and vice-versa: just swap the order of the operations. An (α, β, γ) rotation using X-Y-Z intrinsic convention is equivalent to a (γ, β, α) rotation using Z-Y-X extrinsic convention; this is true for all Euler or Tait-Bryan axis combinations.
Geometric derivation
The fastest way to get the Euler Angles of a given frame is to write the three given vectors as columns of a matrix and compare it with the expression of the theoretical matrix (see later table of matrices). Hence the three Euler Angles can be calculated.
Nevertheless, the same result can be reached avoiding matrix algebra, which is more geometrical. Assuming a frame with unitary vectors (X, Y, Z) as in the main diagram, it can be seen that:
and since 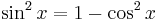
as  is a double projection of an unitary vector:
is a double projection of an unitary vector:
There is a similar construction for  , projecting it first over the plane defined by the axis Z and the line of nodes. As the angle between the planes is
, projecting it first over the plane defined by the axis Z and the line of nodes. As the angle between the planes is 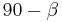 and
and 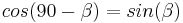 , this leads to:
, this leads to:
and finally, using the cosine inverse function arc cos:
It is interesting to note that the cosine inverse function yields two possible values for the argument. In this geometrical description only one of the solutions is valid. When Euler angles are defined as a sequence of rotations all the solutions can be valid, but there will be only one inside the angles ranges. This is because the sequence of rotations to reach the target frame is not unique if the ranges are not previously defined.[3]
For computational purposes, it may be useful to represent the angles using atan2(y,x):
Relationship with physical motions
- See also Givens rotations
Euler angles can be considered as the result of three composed rotations and these conventions are named according to this composition. Since intrinsic rotations produce the same result as extrinsic rotations inverted, there are two possible names for any static convention. For example the intrinsic ZXY and the extrinsic yxz have the same static parameters.
Euler angles as composition of intrinsic rotations
Starting with an initial set of mobile axes, say XYZ overlapping the reference axes xyz, a composition of three intrinsic rotations (rotations only about the mobile frame axes, assuming active composition) can be used to reach any target frame with an origin coincident with that of XYZ from the reference frame. The value of the rotations are the Euler Angles.
The position of the mobile axes can be reached using three rotations with angles α, β, γ in three ways equivalent to the former definition, as follows:
The XYZ system rotates while the xyz is fixed. Starting with the XYZ system overlapping the reference frame xyz, the same rotations as before can be performed using only rotations around the mobile axes XYZ.
- Rotate the XYZ-system about the Z-axis by α. The X-axis now lies on the line of nodes.
- Rotate the XYZ-system again about the now rotated X-axis by β. The Z-axis is now in its final orientation, and the x-axis remains on the line of nodes.
- Rotate the XYZ-system a third time about the new Z-axis by γ.
Any convention for proper Euler angles is equivalent to three such rotations, with one axis being repeated (ZXZ for example). Tait-Bryan angles are also equivalent to three composed rotations, but in this case, all three rotations are around different axes (ZXY).
Usually conventions are named according with this equivalence.
Euler angles as composition of extrinsic rotations
Also composition of extrinsic rotations (rotations about the reference frame axes, assuming active composition) can be used to reach any target frame. Let xyz system be fixed while the XYZ system rotates. Start with the rotating XYZ system coinciding with the fixed xyz system.
- Rotate the XYZ-system about the z-axis by γ. The X-axis is now at angle γ with respect to the x-axis.
- Rotate the XYZ-system again about the x-axis by β. The Z-axis is now at angle β with respect to the z-axis.
- Rotate the XYZ-system a third time about the z-axis by α. The first and third axes are identical.
This can be shown to be equivalent to the previous statement:
Let us call (e), (f), (g), (h), the successive frames deduced from the initial (e) reference frame by the successive intrinsic rotations described above. We call u, v, w, t, the successive vectors obtained with that rotation. We write 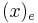 for the column matrix representing a vector x in the frame (e). If necessary we add also a lower index to any matrix we wish to operate in a specific frame. We call
for the column matrix representing a vector x in the frame (e). If necessary we add also a lower index to any matrix we wish to operate in a specific frame. We call 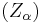 ,
, 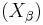 ,
, 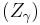 the successive rotations of our example. Thus we can write when describing the intrinsic operations :
the successive rotations of our example. Thus we can write when describing the intrinsic operations :
When describing the intrinsic rotations in the (e) reference frame we must of course transform the matrices used to represent the rotations. Then by the rules of matrix algebra we get :
The relation (5) can then of course be interpreted in extrinsic manner as a succession of rotations around the (e) axes.
Again, proper Euler angles repeat an axis and Tait–Bryan angles do not. As before, this kind of composition is non-commutative.
Euler rotations
Euler rotations are defined as the movement obtained by changing one of the Euler angles while leaving the other two constant. Euler rotations are never expressed in terms of the external frame, or in terms of the co-moving rotated body frame, but in a mixture. They constitute a mixed axes of rotation system, where the first angle moves the line of nodes around the external axis z, the second rotates around the line of nodes and the third one is an intrinsic rotation around an axis fixed in the body that moves.
These rotations are called Precession, Nutation, and intrinsic rotation. While they are rotations when they are applied over individual frames, only precession is valid as a rotation operator, and only precession can be expressed in general as a matrix in the basis of the space.
Gimbal analogy
If we suppose a set of frames, able to move each with respect to the former according to just one angle, like a gimbal, there will exist an external fixed frame, one final frame and two frames in the middle, which are called "intermediate frames". The two in the middle work as two gimbal rings that allow the last frame to reach any orientation in space.
Intermediate frames
The gimbal rings indicate some intermediate frames. They can be defined statically too. Taking some vectors i, j and k over the axes x, y and z, and vectors I, J, K over X, Y and Z, and a vector N over the line of nodes, some intermediate frames can be defined using the vector cross product, as following:
- origin: [i,j,k] (where k = i × j)
- first: [N,k × N,k]
- second: [N,K × N,K]
- final: [I,J,K]
These intermediate frames are equivalent to those of the gimbal. They are such that they differ from the previous one in just a single elemental rotation. This proves that:
- Any target frame can be reached from the reference frame just composing three rotations.
- The values of these three rotations are exactly the Euler angles of the target frame.
Relationship to other representations
Euler angles are one way to represent orientations. There are others, and it is possible to change to and from other conventions.
Matrix orientation
Using the equivalence between Euler angles and rotation composition, it is possible to change to and from matrix convention.
Fixed (world) axes and column vectors, with intrinsic composition (composition of rotations about body axes) of active rotations and the right-handed rule for the positive sign of the angles are assumed. This means for example that a convention named (YXZ) is the result of performing first an intrinsic Z rotation, followed by X and Y rotations, in the moving axes (Note: For intrinsic rotations compositions, the order of multiplication of matrices is the opposite of the order in which they're applied to a vector). Its matrix is the product of Rot(Y,θ1) Rot(X,θ2) Rot(Z,θ3) like this:
-
-
-
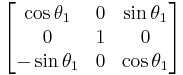 .
.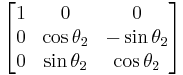 .
.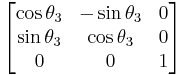
-
-
Subindexes refer to the order in which the angles are applied. Trigonometric notation has been simplified. For example, c1 means cos(θ1) and s2 means sin(θ2). As we assumed intrinsic and active compositions, θ1 is the external angle of the static definition (angle between fixed axis x and line of nodes) and θ3 the internal angle (from the line of nodes to rotated axis X). The following tables can be used both ways, to obtain an orientation matrix from Euler angles and to obtain Euler angles from the matrix. The possible combinations of rotations equivalent to Euler angles are shown here. One table for the left-handed (used for example in computer graphics) convention for the positive sign and one for the right-handed (used for example in dynamics) convention.
Left-handed positive sign convention
-
XZX 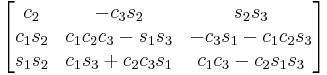
XZY 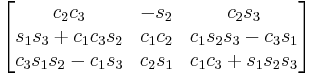
XYX 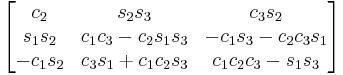
XYZ 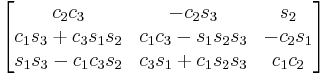
YXY 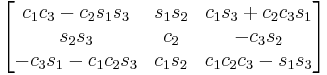
YXZ 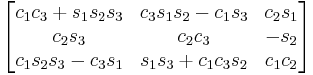
YZY 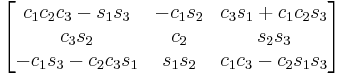
YZX 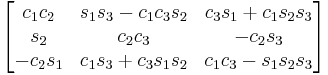
ZYZ 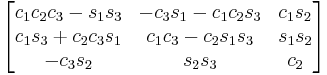
ZYX 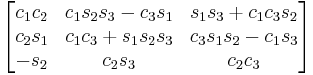
ZXZ 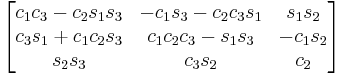
ZXY 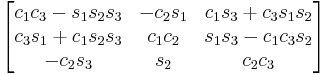
Right-handed positive sign convention
-
XZX 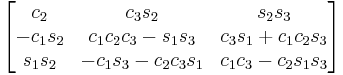
XZY 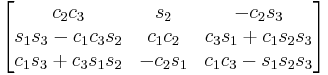
XYX 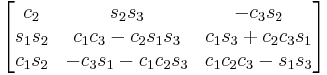
XYZ 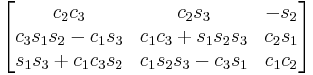
YXY 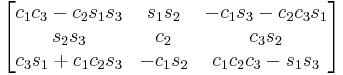
YXZ 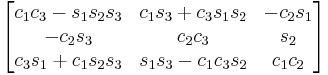
YZY 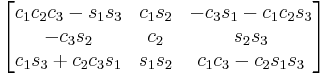
YZX 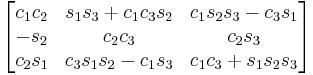
ZYZ 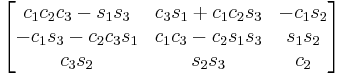
ZYX 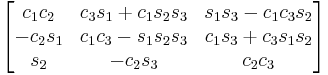
ZXZ 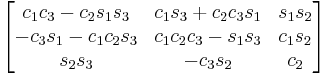
ZXY 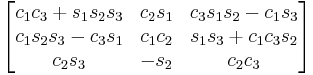
Quaternions
Unit quaternions, also known as Euler–Rodrigues parameters, provide another mechanism for representing 3D rotations. This is equivalent to the special unitary group description.
Expressing rotations in 3D as unit quaternions instead of matrices has some advantages:
- Concatenating rotations is computationally faster and numerically more stable.
- Extracting the angle and axis of rotation is simpler.
- Interpolation is more straightforward. See for example slerp.
Geometric algebra
Other representation comes from the Geometric algebra(GA). GA is a higher level abstraction, in which the quaternions are an even subalgebra. The principal tool in GA is the rotor ![\bold\R=[\cos(\theta/2)-I u \sin(\theta/2)]](/2012-wikipedia_en_all_nopic_01_2012/I/384725346cf78b016c32224991af589c.png) where
where 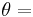 angle of rotation,
angle of rotation, 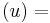 rotation axis (unitary vector) and
rotation axis (unitary vector) and 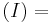 pseudoscalar (trivector in
pseudoscalar (trivector in 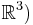
Properties
The Euler angles form a chart on all of SO(3), the special orthogonal group of rotations in 3D space. The chart is smooth except for a polar coordinate style singularity along β=0. See charts on SO(3) for a more complete treatment.
The space of rotations is called in general "The Hypersphere of rotations", though this is a misnomer: the group Spin(3) is isometric to the hypersphere S3, but the rotation space SO(3) is instead isometric to the real projective space RP3 which is a 2-fold quotient space of the hypersphere. This 2-to-1 ambiguity is the mathematical origin of spin in physics.
A similar three angle decomposition applies to SU(2), the special unitary group of rotations in complex 2D space, with the difference that β ranges from 0 to 2π. These are also called Euler angles.
The Haar measure for Euler angles has the simple form sin(β)dαdβdγ, usually normalized by a factor of 1/8π².
For example, to generate uniformly randomized orientations, let α and γ be uniform from 0 to 2π, let z be uniform from −1 to 1, and let β = arccos(z).
Higher dimensions
It is possible to define parameters analogous to the Euler angles in dimensions higher than three.
The number of degrees of freedom of a rotation matrix is always less than the dimension of the matrix squared. That is, the elements of a rotation matrix are not all completely independent. For example, the rotation matrix in dimension 2 has only one degree of freedom, since all four of its elements depend on a single angle of rotation. A rotation matrix in dimension 3 (which has nine elements) has three degrees of freedom, corresponding to each independent rotation, for example by its three Euler angles or a magnitude one (unit) quaternion.
In SO(4) the rotation matrix is defined by two quaternions, and is therefore 6-parametric (three degrees of freedom for every quaternion). The 4x4 rotation matrices have therefore 6 out of 16 independent components.
Any set of 6 parameters that define the rotation matrix could be considered an extension of Euler angles to dimension 4.
In general, the number of euler angles in dimension D is quadratic in D; since any one rotation consists of choosing two dimensions to rotate between, the total number of rotations available in dimension D is 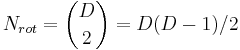 , which for D=2,3,4 yields
, which for D=2,3,4 yields 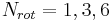 .
.
Applications
Vehicles and moving frames
Their main advantage over other orientation descriptions is that they are directly measurable from a gimbal mounted in a vehicle. As gyroscopes keep their rotation axis constant, angles measured in a gyro frame are equivalent to angles measured in the lab frame. Therefore gyros are used to know the actual orientation of moving spacecrafts, and Euler angles are directly measurable. Intrinsic rotation angle cannot be read from a single gimbal, so there has to be more than one gimbal in a spacecraft. Normally there are at least three for redundancy. There is also a relation to the well-known gimbal lock problem of Mechanical Engineering [4] .
The most popular application is to describe aircraft attitudes, normally using a Tait–Bryan convention so that zero degrees elevation represents the horizontal attitude. Tait–Bryan angles represent the orientation of the aircraft respect a reference axis system (world frame) with three angles which in the context of an aircraft are normally called Heading, Elevation and Bank. When dealing with vehicles, different axes conventions are possible.
When studying rigid bodies in general, one calls the xyz system space coordinates, and the XYZ system body coordinates. The space coordinates are treated as unmoving, while the body coordinates are considered embedded in the moving body. Calculations involving acceleration, angular acceleration, angular velocity, angular momentum, and kinetic energy are often easiest in body coordinates, because then the moment of inertia tensor does not change in time. If one also diagonalizes the rigid body's moment of inertia tensor (with nine components, six of which are independent), then one has a set of coordinates (called the principal axes) in which the moment of inertia tensor has only three components.
The angular velocity of a rigid body takes a simple form using Euler angles in the moving frame. Also the Euler's rigid body equations are simpler because the inertia tensor is constant in that frame.
Others
Euler angles, normally in the Tait–Bryan convention, are also used in robotics for speaking about the degrees of freedom of a wrist. They are also used in Electronic stability control in a similar way.
Gun fire control systems require corrections to gun-order angles (bearing and elevation) to compensate for deck tilt (pitch and roll). In traditional systems, a stabilizing gyroscope with a vertical spin axis corrects for deck tilt, and stabilizes the optical sights and radar antenna. However, gun barrels point in a direction different from the line of sight to the target, to anticipate target movement and fall of the projectile due to gravity, among other factors. Gun mounts roll and pitch with the deck plane, but also require stabilization. Gun orders include angles computed from the vertical gyro data, and those computations involve Euler angles.
Euler angles are also used extensively in the quantum mechanics of angular momentum. In quantum mechanics, explicit descriptions of the representations of SO(3) are very important for calculations, and almost all the work has been done using Euler angles. In the early history of quantum mechanics, when physicists and chemists had a sharply negative reaction towards abstract group theoretic methods (called the Gruppenpest), reliance on Euler angles was also essential for basic theoretical work.
In materials science, crystallographic texture (or preferred orientation) can be described using Euler angles. In texture analysis, the Euler angles provide the necessary mathematical depiction of the orientation of individual crystallites within a polycrystalline material, allowing for the quantitative description of the macroscopic material. [5] The most common definition of the angles is due to Bunge and corresponds to the ZXZ convention. It is important to note, however, that the application generally involves axis transformations of tensor quantities, i.e. passive rotations. Thus the matrix that corresponds to the Bunge Euler angles is the transpose of that shown in the table above. [6]
Many mobile computing devices contain accelerometers which can determine these devices' Euler angles with respect to the earth's gravitational attraction. These are used in applications such as games, bubble level simulations, and kaleidoscopes.
See also
- Rotation representation
- Euler's rotation theorem
- Quaternions
- Axis angle
- Simultaneous orthogonal rotations angle
- Conversion between quaternions and Euler angles
- Quaternions and spatial rotation
- Spherical coordinate system
- Camera transform
Notes
- ^ Novi Commentarii academiae scientiarum Petropolitanae 20, 1776, pp. 189–207 (E478) pdf
- ^ Mathworld does a good job describing this issue
- ^ Gregory G. Slabaugh, Computing Euler angles from a rotation matrix
- ^ The relation between the Euler angles and the Cardan suspension is explained in chap. 11.7 of the following textbook: U. Krey, A. Owen, Basic Theoretical Physics – A Concise Overview, New York, London, Berlin, Heidelberg, Springer (2007) .
- ^ Kocks, U.F.; Tomé, C.N.; Wenk, H.-R. (2000), Texture and Anisotropy: Preferred Orientations in Polycrystals and their effect on Materials Properties, Cambridge, ISBN 9780521794206
- ^ Bunge, H. (1993), Texture Analysis in Materials Science: Mathematical Methods, CUVILLIER VERLAG, ASIN B0014XV9HU
References
- Biedenharn, L. C.; Louck, J. D. (1981), Angular Momentum in Quantum Physics, Reading, MA: Addison–Wesley, ISBN 978-0-201-13507-7
- Goldstein, Herbert (1980), Classical Mechanics (2nd ed.), Reading, MA: Addison–Wesley, ISBN 978-0-201-02918-5
- Gray, Andrew (1918), A Treatise on Gyrostatics and Rotational Motion, London: Macmillan (published 2007), ISBN 978-1-4212-5592-7
- Rose, M. E. (1957), Elementary Theory of Angular Momentum, New York, NY: John Wiley & Sons (published 1995), ISBN 978-0-486-68480-2
- Symon, Keith (1971), Mechanics, Reading, MA: Addison-Wesley, ISBN 978-0-201-07392-8
- Landau, L.D.; Lifshitz, E. M. (1996), Mechanics (3rd ed.), Oxford: Butterworth-Heinemann, ISBN 978-0-7506-2896-9
External links
- Weisstein, Eric W., "Euler Angles" from MathWorld.
- Java applet for the simulation of Euler angles available at http://www.parallemic.org/Java/EulerAngles.html.
- http://sourceforge.net/projects/orilib – A collection of routines for rotation / orientation manipulation, including special tools for crystal orientations.
- (Italian) A generalization of Euler Angles to n-dimensional real spaces
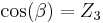
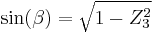
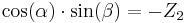
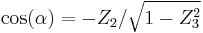
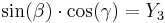
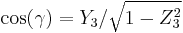
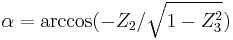
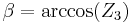
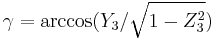
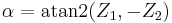
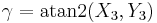
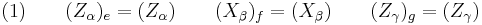
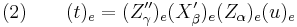
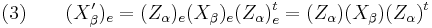
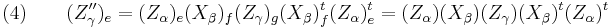
![(5) \qquad (t)_e = [(Z_\alpha)(X_\beta)(Z_\gamma)(X_\beta)^t (Z_\alpha)^t] [(Z_\alpha)(X_\beta)(Z_\alpha)^t] (Z_\alpha) (u)_e = (Z_\alpha) (X_\beta) (Z_\gamma) (u)_e](/2012-wikipedia_en_all_nopic_01_2012/I/c1f3671621e1b2e9fadaf978639b8df1.png)